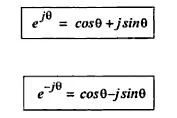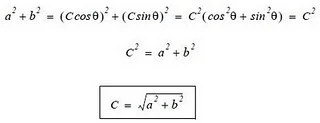YGS Matematik - Mutlak Değer Konu Anlatımı

Mutlak Değer Konu Anlatımı

YGS Matematik - Köklü Sayılar Konu Anlatımı

YGS Matematik - Köklü Sayılar

YGS Matematik Oran- Orantı - I

ORAN - ORANTI KONU ANLATIMI

Microsoft'un Yeni İşletim Sistemi Windows 8

Ve sonunda Windows 8 indirilmeye hazır. Microsoft'un en yeni işletim sistemini ücretsiz olarak indirmek için tek tıklama yetiyor. İşte detaylar.

Son günlerin gündemden düşmeyen konusu Windows 8'den haberler gelmeye devam ediyor. Eklediği çok sayıda özellik ile kullanıcıların beğenisini kazanan Microsoft, sonunda Windows 8'in indirilebilir sürümünü yayımladı. Basit bir şekilde temel işlevleri gerçekleştirip arayüzü tanıyabileceğiniz işletim sistemi, inceleyen hemen hemen herkesi kendine aşık etmiş durumda.

 Windows 8'i indirmek için buraya tıklayın.

Windows 8 Developer Preview English, 32-bit (x86)

DOWNLOAD (2.8 GB)
Sha 1 hash - 4E0698BBABE01ED27582C9FC16AD21C4422913CC
Includes a disk image file (.iso) to install the Windows 8 Developer Preview and Metro style apps on a 32-bit PC.
Note: This download does not include developer tools. You must download the Windows 8 Developer Preview with developer tools 64-bit (x64) to build Metro style apps.

Windows 8 Developer Preview English, 64-bit (x64)

DOWNLOAD (3.6 GB)
Sha 1 hash – 79DBF235FD49F5C1C8F8C04E24BDE6E1D04DA1E9
Includes a disk image file (.iso) to install the Windows 8 Developer Preview and Metro style apps on a 64-bit PC.
Note: This download does not include developer tools. You must download the Windows 8 Developer Preview with developer tools 64-bit (x64) to build Metro style apps.

Einstein'ın Beynindeki 3 Önemli Fark

Bilim adamları, 1955′te ölen Einstein’in cesedini yakmışlar, beynini araştırmalar için almışlardı. Yapılan araştırmalarda Einstein’in beyninin 3 önemli farkının olduğu ortaya çıktı.

Elbetteki sizinkinden daha büyük. Fakat farklı bir şekli olduğunu da söyleyebiliriz.

Şüphesiz Albert Einstein’in zekası bütün zamanların en iyilerinden biridir. Bugünlerde bilim adamları, Einstein’in kavramları işlemede sadece eşsiz bir beyin yeteneğine sahip olmadığını aynı zamanda beyninin fiziksel olarak da farklı olduğunu söylüyorlar.

Einstien’in beyin özellikleriyle, benzer yaştaki dört insanın beyin özelliklerini karşılaştıran yeni bir araştırmada yapısal farklılıklar bulundu. Daha önce araştırma yapan bilim adamları, Einstein’in daha fazla beyin hücrelerine sahip olduğunu belirtirken, bu araştırma beyninin diğerlerinden daha büyük olduğunu ortaya çıkardı.

1955’de 76 yaşında ölen bu büyük matematikçi ve fizikçinin beyni, uzun yıllar boyunca araştırmacıların ilgisini çekmiştir. Einstein’in cesedi yakıldı, sadece beyni bilimsel çalışmalar için korunmuştu.

Diğer araştırmacılar Einstien’in beyninin her bir nöronunda çok sayıda glial ( sinir sistemi destek dokusu) hücrelerinin olduğunu ve bu hücrelerin daha çok enerjiye ihtiyacı olduğunu ve enerji kullandığını bulmuşlardı. Bunun sonucu olarak beyin daha geniş çalışma kapasitesine ulaşır. Glial hücrelerinin vazifesi nöronlar için gerekli destek ve korumayı sağlamaktır.

Önceki araştırma, Einstein’in beynindeki nöronların yoğunluğunun daha büyük olduğu ve beyin zarının diğerlerinden daha ince olduğunu göstermişti.

Aynı zamanda Einstein’in, beynin matematik becerisinin olduğu varsayılan bölgede olağandışı bir tarzda oluklar olduğu ve diğer beyinlerden yüzde 15 daha büyük olduğu bulunmuştu. Farklılıkların kombine etkisi, matematiksel alana ait sinir hücreleri arasındaki bağlantıların daha iyi olmasına yol açmış olabilirdi.
Bu hafta yayınlanan en son araştırmaya ABD ve Arjantin’den bilim adamları katıldılar.
Araştırmacılar, “Einstein’in astrositik (merkezi sinir sistemindeki yıldız şekilli glial hücre) çıkıntılarının tabakalar arası terminal kitlelerinin boyutlarının daha büyük ve sayısının daha çok olduğunu” belirtiyorlar.  Bu farklılıkları tam olarak neyin etkilediği tam olarak belli değil. Araştırmacılar, bulduklarının basit bir yaşlanmanın işareti de olabileceğini hatırlatıyorlar.

Bununla birlikte araştırmacılar, Einstien’in beyninin benzersiz olamayabileceğini ve diğer insanlarında benzer beyne sahip olabileceğini, ancak hiçbir zaman aynı derecede kullanamayacaklarını belirtiyorlar:
“Belki de ‘özel’ beyin ve zekaya sahip birey sayısı sanılandan da fazla. Bunlar; sosyo-kültürel şartlar, hastalıklar sebebiyle beynin bu kapasitesinin pasifleşmesi, gebelik döneminde bebeğin risk altında olması, veya çocuğun büyüdüğü ortamın yetersiz olması sebebiyle görülemeyebilir.”
Araştırmacılar, beynin tek başına zeka derecesinin bir göstergesi olarak görülmemesi gerektiğini söylüyorlar. “Yoğun sosyal içerikli beyin ve zekaya sahip türler, örneğin insanlar, çoklu genetik ve çevresel faktörlere bağlı olarak bireyin özel yeteneğinin gelişebileceğini” belirtiyorlar.
Farklılıklar
1 – Önceki araştırmacılara göre, Einstein’in beyin zarı daha ince ve aynı yaştaki birisine kıyasla yüzde 15 daha büyüktü. Aynı zamanda glial olarak adlandırılan sinir doku hücre sayısı, ortalamadan daha fazla bulunmaktaydı.
2 – Einstein’in beyin dokusu daha büyük boyutta ve nodüller ( terminal kitleler) daha fazla sayıdadır. Böyle olması, onun beynini tam olarak nasıl etkilediği tam olarak bilinmiyor. Belki de bu, yaşlanmanın bir belirtisi de olabilir.
3 – Einstein’deki nodül miktarı başka insanlarda da bulunabilir. Hatta, benzer beyne de sahip olabilirler. Ancak, potansiyelleri ortaya çıkarma şansına sahip olamayabilirler.

Matlab'da Kompleks Sayılar

Herkese Merhabalar,

  Şimdi diyeceksiniz ki ne gerek var böyle şeylere, ancak demeyin öyle! İlerleyen zamanlarda göreceğimiz teorileri anlayabilmek ve simule edebilmek için kompleks sayılar ve matrisleri kısaca hatırlayacağız. Bu yazımda kompleks sayılar ve Matlab da ilgili fonksiyonlar üzerinde duracağım. Matrisler ise bir sonraki konu...

   Hepimizin bildiği gibi matematikte i karakteri kök içinde -1 e eşittir. Ancak bu yazımda  i yerine daha çok j yi kullanacağım. Aslında bu j başka bir değerle çarpıldığında (vektörle çarpıldığında) saat yönünün tersinde 90 derece dönmesine sebep olur. Aşağıdaki şekil üzerinden anlamaya çalışalım. 

Şekilde görüldüğü gibi A vektörü x ekseninin pozitif kısmında bulunmaktadır. A vektörünü her j ile çarpışımızda saat yönünün tersinde 90 derece dönmektedir. Hatırlayacağınız gibi x eksenine reel kısım, y eksenine ise imajiner kısım diyoruz. Bu durumda eğer A=a+jb şeklinde bir vektörümüz olursa a=Re{A} ve b=Im{A} olacaktır. Kompleks sayılar üzerinde toplama ve çıkarma yaparken reel kısımlar ve imajiner kısımlar birbirleriyle toplanır veya çıkarılır, yani reel kısımlarla imajiner kısımlar arasında işlem yapılmaz. Aşağıdaki şekilde bu durum gösterilmiştir.

Kompleks sayılar çarpılırken ise dağılma özelliği esas alınır.

Bir kompleks sayının hatırlayacağınız üzere birde eşleniği bulunmaktadır.

a

+jb şeklinde bir kompleks sayının eşleniği

a-jb şeklindedir. Matlabda eşlenik almak için conj() fonksiyonunu kullanırız.

 Eşleniği alınan bir kompleks sayının reel kısmının yönü sabit kalıp, imajiner kısmı 180 derece ters döner. Kompleks sayılar için bölme işleminde ise paydada ki kompleks değerin eşleniği alınır ve hem pay hemde payda bu değer ile çarpılır. A=a+jb kompleks sayısını, B=c+jd sayısına bölme işlemi aşağıda ki gibidir.

Şimdi gelelim kompleks sayıların üstsel(eksponansiyel) ve polar formda gösterimlerine. Aşağıdaki şekilde ki gösterime hatırlayacağınız gibi Euler açılımı diyoruz. 

 Eğer bu kompleks sayıları C ile gösterdiğimiz bir sabitle çarparsak şu şekli alır;

Yukarıda ki eşitlik bir kompleks sayıyı temsil etsin ve bu sayıya a+jb diyelim. Bu durumda

 şeklinde olacaktır. Bu durumda a = Ccosθ ve b = Csinθ olacaktır. Reel ve imajiner kısımdaki sayıların karelerini alır ve toplarsak

bu kompleks sayının genliğini bulmuş oluruz. b yi a ya oranladığımızda ise  

kompleks sayımızın açısını elde ederiz. Sonuç olarak diktörtgensel formdan üstsel forma geçiş için;

üstsel formdan dikdörtgensel forma geçmek için;

eşitliklerini kullanırız. Polar formda gösterim biçimi ise;

şeklindedir. Ayrıca unutulmaması gereken bir nokta ise açıyı hesaplarken her zaman pozitif x eksenini referans olarak alırız. 

   

Şimdi bir örnekle bu öğrendiklerimizi Matlab da nasıl uygulayabiliriz onu anlamaya çalışalım. y=-1+j2 kompleks sayısını reel ve imajiner eksende ifade edersek aşağıdaki şekilde ki gibi bir sonuç elde ederiz.

Burada kök 5 değeri y vektörünün genlik değerini gösterirken 116.6 derece ise x ekseninin pozitif kısmı referans alınması durumunda açısını gösterir.  Matlab da bir komplek sayının genliğini bulmak için abs() açısını bulmak için angle() fonksiyonunu kullanırız. Burada unutulmaması gereken Matlab ın angle() fonksiyonu ile hesapladığı değer derece değil radyan cinsindendir. Dolayısıyla sonucu derece cinsinden görmek için angle(y)*180/pi şeklinde kullanmalıdır. Aşağıda Matlab örneği gösterilmiştir.

ÖZ-DE-BİR 8. Sınıf SBS Çözümleri

ÖZ-DE-BİR 8. Sınıf Türkiye Geneli SBS Matematik Soru Çözümleri 

21 OCAK 2011

                                                                                 Tüm Çözümler için Tıklayınız ...

MATLAB ile fonksiyon yazma

Matlab'da fonksiyonlar ayrı bir dosyadan çağrılabileceği gibi , fonksiyonlar da m-dosyalarıdır. Farklı olarak bir fonksiyonun ilk satırı söyle olmalıdır:

function [sonuc1, sonuc2, ..., sonucm] = 

fonksiyonmbardak(arg1, arg2,...,argn)

Fonksiyonun adı dosya adı ile aynı olmalıdır. Örnegin "fonksiyonm"bardak fonksiyonu "fonksiyonmbardak.m" dosyasına koyulmalıdır. Örnek olarak fonksiyonmbardak.m ve digerfonksiyonum.m dosyalarına bakiniz.

Fonksiyonlar lokal ortamda çalıştırırlar. Yani ana calışma alanındaki aynı isimdeki bir değişkeni kaybetme riskiniz yoktur. Fonksiyonun sonucunda sadece sonuc olarak dönen deüişkenler, çağıran fonksiyonun çalışma alanında görülür.

Örnekleri yapmadan önce aşağıdaki fonksiyonları çalışma dizininize kaydedin.

fonksiyonmbardak.m:

2 girdi argumanı alan ve 2 değer döndüren örnek fonksiyon

function [y, z] = digerfonksiyonum(a, b)
y = a + b;
z = a - b;

Kullanımı :a = [1 2 3 4];
           b = fonksiyonmbardak(2 * a)
           a

 Görüldüğü üzere a değeri değişmedi. Şimdi de iki değişken döndüren örneğimizi çağıralım.

[c, d] = digerfonksiyonum(a, b)

c =

1 5 9 13

d =

1    -1    -3    -5

12.01.2011 //  03:19

LaTeX'te birkaç matematiksel formül tüyosu

LaTeX'te daha güzel formüller elde etmek için birkaç matematik formülü yazma tüyosu :)

1. LaTeX'te denklemlerde toplama, integral, limit gibi sembollerin altına i=1->inf gibi şeyler yazmak istendiğinde altına değil de sağ alt köşeye yazar ya latex onu, tam altına yazdırmak için birkaç yöntem vardır. Birincisi denklemi iki dolar arasına koymak, ama bu denklemi 'inline' olmaktan çıkarır ve ortaya hizalar. İkincisi \displaystyle kullanmak. Şöyle ki; görünümünü düzeltmek istediğimiz toplama işaretlerinin başına \displaystyle yazıyoruz. Aslında her toplama işaretinin başına yazmak gerekli değil, bir kere yazarsak tüm satırdaki toplama işaretlerini düzeltiyor, ama satırın anlamı değişebiliyor. Örneğin, bölme çizgisi kullanılacaksa, \frac{}{} yapısında her parantezin içine \displaystyle yazmak gerekiyor. Ya da array'lerde her satır ve sütun için, yani her & ve \\ işaretinden önce de \displaystyle yazmak gerekiyor. Üçüncü yöntem de \limits kullanmak.
2. Çift ya da üçlü integral yaparken \int\int\int demek yerine \iiint, \int\int demek yerine \iint denildiğinde integraller birbirlerine yapışıyorlar. Özellikle teker teker her integral için limit değerler yazılmayacaksa çok faydalı oluyor. Bunlar, amsmath paketindeler.
3. Büyük bir bölme işlemini, hatta alt alta yazılmış bir array'i parantez içine almak icin \left \right kullanımı parantezlerin boyunu büyütüyor. Örneğin, a = { 0 if a<0, 1 if a>=1 gibi bir şey yazmak istedik. 0 if a<0, 1 if a>=1 ifadesini bir array'e yazarız. Bu array'in başına \left\{ sonuna ise \right. yazarız, yani sağ tarafa parantez koymak istemiyorsak \right'tan sonra nokta koymak gerekir. Böylece parantez tüm array'i kaplar, ortada küçücük kalmaz. 12.01.2011 : 02:15 uyku vakti ...

Farktal Kavramı...

Fraktal'ın Kelime Anlamı 

Fraktal parçalanmış ya da kırılmış anlamına gelen Lâtince fractus kelimesinden gelmiştir. İlk olarak 1975'de Polonya asıllı matematikçi Benoit Mandelbrot tarafından ortaya atıldığı varsayılır. Kendi kendini tekrar eden ama sonsuza kadar küçülen sekilleri, kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününü inceler. Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza kadar sürebilir; tam tersi de her parçanın her bir parçası büyütüldüğünde, gene cismin bütününe benzemesi olayıdır. Doğada görebilen örnekler örneğin bazı bitkilerin yapısı dir.

Fraktal ve Fraktal Geometri nedir?
İlk matematiksel fraktal kavramı 1861 de keşfedildi. Karl Weierstrass sürekli fakat hiçbir noktada

diferensiyellenebilir olmayan , yani köşe noktalarından oluşan bir eğri üzerindeki değişmeleri araştırken, hiçbir noktada değişme oranının bulunamayacağı kanaati ile sarsılmıştır. Fraktal kelimesini Weierstrass bu cins eğriler için ilk defa kullanmıştır.
Matematik anlamda ilk çalışılan fraktal, Cantor Cümlesidir. Cantor (1845-1918) Halle Üniversitesi'ndeyken matematiğin temel konularından olan ve günümüzde Cümle Teorisi olarak adlandırılan alanı kuran bir Alman matematikçidir.
Fraktalların tarihi gelişiminde Cantor, Sierpinski, Von Koch, Peano gibi matematikçiler tarafından oluşturulan fraktallar matematiksel canavarlar olarak adlandırılır. Matematiksel canavarların bahçesinde veya ilk fraktalların ortaya çıktığı zamanlarda Cantor cümlesi görünüş açısından diğerlerinden daha az gösterişli olmasına ve diğerlerine göre doğal yoruma daha uzak olmasına rağmen oldukça önemlidir. Cantor cümlesinin, matematiğin pek çok alanında özelikle Kaotik Dinamik Sistemlerde önemli rol oynadığı ve pek çok fraktallar (Julia cümleleri gibi) için de gerekli bir model olduğu görülmektedir.
Etrafımızda, parlak, tuhaf, güzel şekilli cisimler görürüz. Bunlara Fraktal denir. Gerçekten bunlar nedir?
İnternette fraktallar hakkında çok fazla bilgi vardır, fakat bu bilgilerin büyük kısmı ya güzel resimler veya yüksek seviyeli matematiksel kavramlarla ilgilidir. Dolayısıyla kolayca anlaşılır bir ifade ile diyebiliriz ki fraktallar tuhaf resimleri olan cisimler, matematiksel nesnelerdir. Okulda karşılaştığımız matematiğin çoğu eski bilgilerdir. Örneğin, geometride karşılaştığımız çemberler, dörtgenler ve üçgenler M.Ö. 300 üncü yıllarında Öklid tarafından ortaya konulmuştur. Buna rağmen Fraktal Geometri daha çok yenidir. Fraktallar üzerinde matematikçiler tarafından araştırmalar son 25 yıldır başlamış bulunmaktadır.



Fraktal; matematikte, çogunlukla kendine benzeme özelligi gösteren karmasik geometrik sekillerin ortak adidir. Fraktallar, klasik, yani Eukleidesçi geometrideki kare , daire , küre gibi basit sekillerden çok farklidir. Bunlar, dogadaki, Eukleidesçi geometri araciligiyla tanimlanamayacak pek çok uzamsal açidan düzensiz olguyu ve düzensiz biçimli tanimlama yetenegine sahiptir. Fraktal terimi “parçalanmis” yada “kirilmis” anlamina gelen Latince "fractus" sözcügünden türetilmistir. Ilk olarak 1975’te Polonya asilli matematikçi Beneoit B. Mandelbrot tarafindan ortaya atilan fraktal kavrami, yalnizca matematik degil fiziksel kimya, fizyoloji ve akiskanlar mekanigi gibi degisik alanlar üzerinde önemli etkiler yaratan yeni bir geometri sisteminin dogmasina yol açmistir.
Tüm fraktallar kendine benzer ya da en azindan tümüyle kendine benzer olmamakla birlikte, çogu bu özelligi tasir. Kendine benzer bir cisimde cismi olusturan parçalar ya da bilesenler cismin bütününe benzer. Düzensiz ayrintilar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza degin sürebilir; öyle ki,her parçanin her bir parçasi büyütüldügünde, gene cismin bütününe benzer. Bu fraktal olgusu, kar tanesi ve agaç kabugunda kolayca gözlenebilir. Bu tip tüm dogal fraktallar ile matematiksel olarak kendine benzer olan bazilari, stokastik, yani rastgeledir; bu nedenle ancak istatistiksel olarak ölçeklenirler. Fraktal cisimler,düzensiz biçimli olduklarindan ötürü Eukleidesçi sekilleri ötelenme bakisina sahip degildirler. (Ötelenme bakisimina sahip bir cisim kendi çevresinde döndürüldügünde görünümü ayni kalir.)
Fraktallarin bir baska önemli özelligi de, fraktal boyut olarak adlandirilan bir matematiksel parametredir. Bu cisim ne kadar büyütülürse büyütülsün ya da bakis açisi ne kadar degistirilirse degistirilsin, hep ayni kalan fraktallarin bir özelligidir. Eukleidesçi boyutun tersine fraktal boyut, genellikle tam sayi olmayan bir sayiyla, yani bir kesir ile ifade edilir. Fraktal boyut, bir fraktal egri yardimiyla anlasilabilir.
Olusturulmasinin her asamasinda bu tip bir egrinin çevre uzunlugu 4/3 oraninda büyür. Fraktal boyut (D)4'e esit olabilmesi için alinmasi gereken kuvvetini gösterir; yani;
3d =4 bu bakimdan fraktal egriyi niteleyen boyut log4/log3 ya da kabaca 1,26'dir. Fraktal boyut, Eukleidesçi olmayan belirli bir biçimin karmasikligini ve sekil nüanslarini açiga çikarir.
Kendine benzerlik ve tamsayi olmayan boyutlu kavramlariyla birlikte fraktal geometri, istatistiksel mekanikte, özellikle görünürde rastgele özelliklerden olusan fiziksel sistemlerin incelenmesinde giderek daha yaygin olarak kullanilmaya baslanmistir. Örnegin, gökada kümelerinin evrendeki dagiliminin saptanmasinda ve akiskan burgaçlanmalarina iliskin problemlerin çözülmesinde fraktal benzetimlerden (simülasyon) yararlanilmaktadir. Fraktal geometri bilgisayar grafiklerinde de yararli olmaktadir. Fraktal algoritma ise, engebeli daglik araziler ya da agaçlarin karisik dal sistemleri gibi karmasik, çok düzensiz dogal cisimlerin gerçektekine benzer görüntülerinin olusturulabilmesini olanakli kilmistir.

Fraktal Nedir?

Fraktal, matematikci Bénoit Mandelbrot tarafindan bulunan Mandelbrot kumelerinin ozel bir hali olan Julia Egrilerinin turevlerini cizebilir. En iyi bilinen fraktal bir kar tanesine benzeyen Koch Egrisi dir. Bu egriler iki boyutludur. Iki boyutlu cizim kompleks duzlemde yapilir. C1 sayisi kompleks sayinin reel kismini, C2 sayisi imajiner kismini temsil eder.

Fraktal kelimesi matematiksel anlamda kaotik ortamlarin icerdigi bilgi ile aynidir. Kaotik ortamin matematiksel anlami; sayilamaz coklukta duzenli olaydir.

Matematik Öğrenmek ...

İnternette dolaşırken matematik öğrenme konusu hakkında güzel bir makaleye rastladım. Matematikten gıcık kapanlar ya da öğrenemiyorum diyenlerin en az 1 defa okumasında fayda olduğunu düşünüyorum

Kimyada ‘eşik enerjisi’ diye bir tabir (terim,olgu) vardır. Bir kimyasal tepkimenin başlayabilmesi yada gerçekleşmesi için gerekli minumum enerji miktarı diyebiliriz. Bu enerjiye ulaştıktan sonra tepkime başlar ve devamı gelir.

Fizikte ‘yüzey gerilimi’ diye adlandırılan benim hoşuma giden bir konu var.Kabaca; sıvıların yuzeylerindeki moleküllerin birbirini sıkı sıkıya tutması diyebiliriz.Yüzey gerilimi sayesinde bir iğnenin suyun yüzeyinde yüzmesini sağlayabiliriz, halbuki iğnenin özkütlesi daha büyüktür.Hani bir bardağa ağzına kadar su koyarız, bazen öyle olur ki su seviyesi bardağın seviyesinin birkaç milim üstüne çıktığı halde su dökülmez ve eğri,tombul bir yüzey oluşturur.İşte bunun sebebi suyun yüzey gerilimidir. Moleküller birbirini tutar ve su dökülmez, tıpkı iğneyi tuttukları gibi. Benim hoşuma giden birkaç damla daha su ilave ettikten sonra aniden suyun dayanamayıp kendini bırakarak bardaktan dökülmesidir. Dökülen miktar hepimiz görmüşüzdür; son ilave ettiğimiz damla miktarından daha fazladır.

Bir öğrencinin matematik dersinden gerçek manada başarılı olabilmesi için belli bir eşik enerjisine ulaşması gerekir.Eğer bunu yapabilirse o noktadan sonra ne özel ders,kurs ne de herhangi bir ekstra yardıma gereksinim duyar.Belki bazen ufak tefek, küçük ayrıntılardır takıldığı noktalar. Çok berbat anlatılmamak üzere anlatılan herşeyi rahatça anlar.Kendine güveni tamdır ve çok rahattır.Artık taşmıştır, bardak alması gerekeni almıştır,şifre çözülmüş,resmin tamamı görünmüş, parçalar yerine yerleşmemiş olsa bile yapboz’un tamamı zihinde canlanmıştır.Artık sistemin nasıl işlediği açıktır. Geriye kalan tek şey çalışma azmini ve gayretini kaybetmeyip devamını getirebilmektir. Çünkü işin zor tarafı halledilmiştir.Önemli olan resmin tamamını görebilmektir.

Öğrencinin bu bahsettiğim noktaya gelebilmesi için matematik öğretmeninin yapması gereken şey; meşhur atasözünde söylendiği gibi balık vermekten çok balık tutmayı öğretmektir.Ve öğrencinin yapması gereken de gerekli bilgi ve pratiği kazandıktan sonra bazı şeyleri kendi başına halletmeye çalışmaktır.

Bir matematik konusunu öğrenmek istiyorsanız önce kısa süreli konuya bakarsınız, sonra soru çözmeye başlarsınız.Eğer yeni bir soru çözerken soruyu çözemediğiniz takdirde;
-Defterin sayfalarını karıştırmaktan.
-Kitabın çözümlü örneklerine gözatmaktan.
-Sorunun aynısını bir yerden bulmaya çalışmaktan.
-Soruyu arkadaşınız yada hocanıza götürmekten, önce yapacağınız ilk iş düşünmek… düşünmek …düşünmek olmalıdır.Zekanızın yardımı ile sizin çözdüğünüz bir soru, hem sizin için daha yararlı hemde daha büyük bir zevktir.

Bilgiye ulaşmanın çok hızlı olduğu dünyamızda hafızamızı çok fazla zorlamaya gerek duymuyoruz. Aklımıza takılan birçok şeye internet sayesinde ulaşmak sadece saniyeler alıyor. Beynimizi birçok bilgi ile doldurmaktan vazgeçsek bile unutulmamalıdır ki bilgiyi işleyecek zekaya hepimizin ihtiyacı var. Eğer ailenizden,öğretmenlerinizden,kitaplardan öğrendiğiniz şeyleri sorgulamıyorsanız,üzerinde düşünmüyorsanız siz beyninizi sadece depolama alanı olarak kullanıyorsunuz demektir. Bir bilgisayarın işlemcisi kötü ise harddiskinin kaç gigabyte bilgi depoladığının önemi yoktur.

Bilgiyi sorgulamak demek; itiraz etmek,karşı çıkmak,muhalefet etmek değildir.Bilgiyi sorgulamak bilginin üzerine düşünmek,anlamlar çıkarmak,yeni sonuçlar elde etmek, doğru yada yanlışlığı hakkında şüpheci hareket etmektir. Tahtadaki matematik öğretmenine; bu nerden geldi,şurası niye böyle oldu,bu formul nerden çıktı? diye soran bir öğrenciye başlangıç aşamasında saygı duysam da eğer bu pozitif tutumu bir süre sonra sorduğu sorulara kendisinin cevap aramasına ve bulmasına dönüşmediyse, bu öğrenci aklına takılan herşeyi tüm lise yaşamında hocasından beklemeye devam ettiyse; eşik enerjisine hiçbir zaman ulaşamaz. Tabiki insan hiç bilmediği bir konuda çıkarım yapamaz ve birçok sorunun cevabını bulamaz. Yeni öğrenilen her konuda sorular sormalı,bilginizi pekiştirmelisiniz.Fakat bunu adet edinmişseniz,her zaman hazıra alışırsanız, hayatınız boyunca birilerine muhtaç yaşarsınız.

Matematik dersinini en önemli amacı zekayı geliştirmektir. Eğer siz size öğretilenden daha ileriye gitme konusunda ufacık bir gayret göstermezseniz, tabiki sizin için matematik boş,saçma ve zaman kaybından başka birşey değildir.

Eğer siz başkalarının anlattıklarından,düşüncelerinden,yaşantılarından sonuçlar çıkarmayıp, öğretilen herşeyi körü körüne kabullenirseniz.Başkalarının fikirlerinin sözcüsü olmaktan ileri gidemezsiniz.Kulaklarınızı hiçbirşeye tıkamayın, birisi çıkıp 2+2=5 diyorsa gülüp geçmeyin ciddiye almamazlık etmeyin,dinleyin, empati kurun. Benim bildiğim doğru,diğerleri yanılıyor düşüncesiyle yatıp kalkan biri, karşıdakinin görüşünü anlamaya çalışmaktan çok kendi düşüncesine saplanıp kalmış biri, kaybetmeye mahkumdur.
Bu ülkenin gerçekten düşünen ,sorgulayan,üreten beyinlere ve bir o kadar da iyi niyetli kalplere ihtiyacı var.

Pratik Matematik Teknikleri

Soru Tarzı :

243 Sayfalık bir kitabı numaralandırmak için kaç rakam kullanılır? şeklindeki sorularda çözüm yapılırken önce sayının kaç basamaklı olduğuna bakılır ...

- sonra sayının kendisi ile basamak sayısı çarpılır

- sayının basamak sayısının 2 eksiği kadar 1, yanına 1 adet 0 ve sağına basamak sayısını 11 e tamamlayan sayı yazılarak bu çarpımdan çıkartılır .

örnek çözüm :  243 3 basamaklı olduğundan 

cevap 3x(243) - 108 = 621 olarak bulunur. 

Örnek Soru -1  3548 sayfalık bir kitabı numaralandırmak için kaç adet rakam kullanılır? 

Çözüm :  4x(3548) - 1107 = 13085 bulunur.  farklı örnekler türatilebilir...

                

Pratik Matematik Teknikleri ...

·  Sonu sıfırla biten sayıları çarpmak çok kolaydır. Mesela 3000 ile 500'i çarpmak istediğimizde ilk önce 3 ile 5'i çarpar. Daha sonra 15'in yanına kullanılan sıfır kadar sıfır koyar ve sonucu 1500000 buluruz.

·  Peki 5 ile biten sayıları kendileri ile çarpmak için ne yapmak gerekir? Mesela 75x75 çarpımını göz önüne alalım. Onlar basamağındaki rakam olan 7 ile bir ardılı olan 8'i çarpalım. 56 sayısının yanına birler basamağındaki rakamlar olan 5 ile 5 çarpımını yazalım. Sonuç olarak 75x75 = 5625 buluruz. Aynı şekilde 65x65 = 4225, 85x85=7225 bulunur.

·  Aralarında 2 fark bulunan sayıların çarpımını bulmak için, sayıların ortalamasının karesinin 1 eksiğini alırız. Örneğin 29 ile 31'in çarpımından 30x30 - 1 = 899 bulunur.

·  İki bamaklı bir sayıyı 11 ile çarpmak istediğimizde sayının birler ve onlar basamağındaki rakamları toplar, toplamı iki rakamın arasına yazarız. Örneğin 27x11=297 (2+7=9) buluruz. Eğer toplam 9'dan büyükse yüzler basamağındaki rakamı bir arttırırız. Örneğin 49x11 = 539 buluruz. (4 ile 9'un toplamı 13 olduğundan 539 yazdık).

·  Birler basamağındaki rakamları 1 olan 2 basamaklı iki sayıyı çarpmak istersek ne yapacağız? Örneğin 21x41 çarpımını ele alalım. İki sayının onlar basamağındaki rakamlar olan 2 ve 4'ü ilk önce çarpalım, sonra toplayalım. Sırasıyla çarpımı, toplamı ve sondaki 1 sayısını yan yana yazalım. Böylelikle sonucu 861 buluruz. 31x51 çarpımı için 3x5 =15, 3+5=8 yazarsak çarpımın sonucu 1581 bulunur. Eğer toplam 9'dan büyük olursa çarpıma bir ekleriz. Örneğin 81x91 çarpımı için 8x9=72, 8+9=17. Çarpımın sonucu ise 7371 olur.

·  101, 1001, 10001, ... gibi bir sayı ile bu sayıdan bir basamak küçük A sayısını çarpmak istediğimizde, A sayısını yan yana yazmak yeterlidir. Örneğin 101x79=7979, 1001x278=278278, 10001=4162=41624162'dir.

·  Bir sayıyı 25 ile çarpmak için sayıyı 4'e böleriz. Eğer bölüm kalansız ise bölümü 100 ile çarparız, 1 kalanlı ise bölümün yanına 25 koyarız, 2 kalanlı ise bölümün yanına 50 koyarız, 3 kalanlı ise bölümün yanına 75 koyarız. Örneğin 278x25 çarpımı için 278'i 4'e bölelim. Bölüm 69 kalan 2'dir. O halde çarpımın sonucu 6950

Matematik Öğretimi Bölüm-1

Matematik öðretiminin durumunu belirlemek ve değerlendirmek icin, herşeyden önce, şu iki soruya açık yanıtlar
vermek zorundayız.

a. Matematik nedir?
b. Neden Matematik öğretiyoruz?
Bunlara vereceğimiz yanıtlara göre, matematik öðretiminin hedeflerini çizmek ve bu hedeflere götürecek öðretimin
niteliklerini belirlemek olanağı doğacaktır. Ondan sonra,yürürlükteki matematik öðretiminin durumu incelenebilir,
değerlendirmesi yapılabilir.

Bu nedenle, yazımın ilk iki bölümünde bu soruları yanıtlamaya çalışacağım.bana verilen konu ile söyleyeceklerim arasýndaki ilişkiyi sınırlandırmak gereğini duyuyorum. Matematik Öðretiminin Bugünkü Durumu ve Değerlendirilmesi konularının her ikisi de yüzbinlerce gencin eğitimini ve dolayısıyla ülkenin gelecekteki on yıllarını temelden etkileyecek bir olgudur. Bu büyük olgunun yarattığı sorunların birkaç konuşmayla çözümlenmesine olanak olmadıðı apaçık bir gerçektir. Yeterli uzman, yetki ve mali destekle donatılmış bir örgütle yapılacak bilimsel incelemeler sonunda ancak ortaya çıkarabilecek bu sorunları, burada bilimsel yönüyle ortaya koyamayacağımız ve bilimsel çözüm yolları öneremeyeceğimiz açıktır. Dolayısıyla, sözlerimin, kişisel görüşlerim olmaktan öte bilimsel olma savı taşımadığını, öncelikle, belirtmeliyim.

Matematik öğretiminin nasıl olması gerektiği konusundaki tartışmaların Plato Akademisine kadar; yani 2500 yýl geriye giden bir geçmişi vardır. Örgün eðitimin bütün dünyada yaygınlık kazandığı 20.yüzyıl başlangıcından sonra diğer alanlarda olduğu gibi matematik öðretimi, hem içerik hem öğretim yöntemleri açısından sık sık tartışma ve inceleme konusu ola gelmiştir. Hatta 1899 yýlýnda H.Fehr ve C.A. Laisant tarafından Uluslararası bir komisyon kurulmuştur. (Hawson, pp.88). Bu komisyon, bir yandan tek başlarına yaptıkları  çalışmaları destekliyor, çıkardığı L'Enselgnement Mathematiwque adlı dergisiyle konuya katkıda bulunuyor ve her dört yılda bir toplanan Uluslararası Matematik Kongresinde daha boyutlu tartýþmalar açıyordu. 1960 yıllarında
matematikve fen öðretimi pek çok ülkeede görülmemiş bir önemde gündeme geldi. Ulusal ve Uluslararası Matematik Kongresi, matematik öğretimini konu edinecek bir alt komisyon kurdu. Uluslararası Matematik Öğretimi Komisyonu adını alan bu komisyon þimdi her dört yılda bir toplanmaktadır.İçerik ve yöntem tartışmaları 1960lı yıllardaki hızını kaybetmiş olmakla beraber, o yılların getirdiğe denemelerin ışığında olmakla beraber, o yılların getirdiği denemelerin ışığında daha serinkanlı çalışmaların sürdürüldüğü bir gerçektir.

Ülkemizde de matematik öğretimi konusu, hemen hemen ileri ülkelerle birlikte ele alınmış ve değişik projeler ve denemeler yapılmıştır. Bu çalışmalar sonunda, adına Modern Matematik denilen yeni bir öğretim izlencesi (müfredat) hazırlanmış ve bütün ortaöğretimde yürürlüğe konulmuştur.